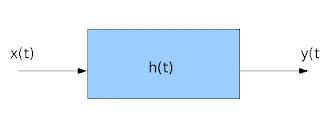
Supondo que a entrada x(t) seja um impulso (Função Delta de Dirac) delta(t).
A função impulso é definida nula para t diferente de 0 e de valor infinito para t em 0. De modo que a área sob a curva seja unitária.
Fazendo a Transformada de Fourier da entrada:
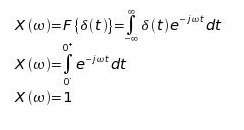
observa-se que esta compreende todas as frequências do expectro. Pelo princípio da superposição, a saída será equivalente a somar a saída para cada frequência, de modo que quando a entrada do sistema é um impulso, a saída do sistema contêm informação sobre todas as possíveis entradas. Esta saída é chamada de resposta ao impulso do sistema h(t).
Como apresentado, a saída h(t) apresenta a sobreposição de todas as saídas possíveis.
Nenhum comentário:
Postar um comentário